© 2026 VideoMan | Επικοινωνία/Contact: info@videoman.gr | Privacy Policy | Terms Of Use
More results...
Loading the player...
Η εφαρμογή του Πυθαγορείου θεωρήματος με νερό




 (42) | 30/12/2012 |
(42) | 30/12/2012 | 
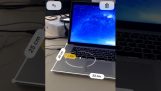
Μια έξυπνη κατασκευή που αποδεικνύει με νερό το Πυθαγόρειο θεώρημα (Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών).
Advanced Related Posts
Οι περισσότεροι 12χρονοι τρελαίνονται να παίζουν βιντεοπαιχνίδια – Ο Τόμας Σουάρεζ έμαθε μόνος του πώς να τα δημιουργεί. Αφού έφτιαξε...
Αυτό είναι το Vantablack, ένα υλικό που κατασκευάζεται από τη βρετανική εταιρεία Surrey NanoSystems και θέτει ένα παγκόσμιο ρεκόρ, απορροφώντας...
Στη νέα έκδοση 12 του λειτουργικού συστήματος της Apple, υπάρχει αυτή η εξαιρετική εφαρμογή μέτρησης σε επαυξημένη πραγματικότητα.
Ένα μωρό ανακαλύπτει τις εφαρμογές του iPhone και συνομιλεί με τον εαυτό του
Στην παραλία Lebon του Ρίο ντε Τζανέιρο στη Βραζιλία, η NIVEA διανέμει στα μικρά παιδιά κούκλες που παθαίνουν ηλιακά εγκαύματα....
Ίσως θυμάστε το Vantablack, το υλικό που απορροφά το 99,965% του ορατού φωτός. Το Vantablack μπορεί να έχει πολλές εφαρμογές,...
Το προφυλακτικό Pronto έχει σχεδιαστεί για αυτούς που βρίσκουν τη διαδικασία εφαρμογής του προφυλακτικού χρονοβόρα, και δίνει την λύση με...
Κάποιος παίζει τη μουσική του Χριστουγεννιάτικου τραγουδιού "Τρίγωνα Κάλαντα" με τον αντίχειρά του στα δόντια μιας χτένας.
Η αστυνομία της Ινδίας έχει μια κάπως αυστηρή μέθοδο εφαρμογής της καραντίνας, καθώς οι παραβάτες δέχονται μερικά χτυπήματα με ένα...
Ένας οινοποιός έφτιαξε ένα αστείο μοντάζ όπου ανοίγει μπουκάλια κρασιών στις νότες του "Τρίγωνα Κάλαντα".
Το Butterfly iQ, ένα φτηνό φορητό εργαλείο υπερήχων, μπορεί να φέρει επανάσταση στην ιατρική εξέταση υπερήχων, και τελικά να γίνει...
Μόλις λίγους μήνες πριν την κυκλοφορία της πολυαναμενόμενης ταινίας Star Wars 7: The Force Awakens, η αμερικανική εταιρία Sphero προωθεί...
Μια μοχθηρή φάρσα αποφάσισε να κάνει η σύντροφος ενός Τούρκου οπαδού, κατά την διάρκεια του αγώνα Τουρκίας-Κροατίας στο Euro 2016....
Δύο μωρά έχουν μια συζήτηση μέσω της εφαρμογής τηλεδιάσκεψης FaceTime. Ενώ οι μητέρες κρατάτε το κινητό τους τηλέφωνο, τα μωρά...
Η DEEP Robotics είναι μια κινεζική εταιρεία που ιδρύθηκε το 2017 και ειδικεύεται στην ανάπτυξη και εφαρμογή τετράποδων ρομπότ για...














comment on fait ca? Avec quels matériaux
Ez csak simán víz. Ismered a Pitagorasz tételt? Ez arra ad választ. (a2+b2=c2) 3 plexit kocka van középen és egy háromszög alakú, vízet be önttöte az alsó kettöbe, mert az engyenlett szerint ki töltti a c2 kockát, ezt magyarázza el. Püthagorasz nagyon okos volt ő találta ki ezt a tételt.
Really good presentation I really liked it. Thank you for it by the way.
Λάμπρο κατ’αρχάς συγχαρητήρια για την παρουσίαση. Ο συναδελφό σας απλά παρατήρησε οτι ειναι ενα εξαίσιο παράδειγμα προς κατανόηση και απομνημόνευση στους μαθητές. Θα έλεγα ευφηέστατο..διότι είναι τόσο απλό και ξεκάθαρο. Κανείς δεν μίλησε για απόδειξη ακριβείας. ΚΑι εσείς φαντάζομαι όταν σχηματίζεται τα σχήματα στο πίνακα κάνενα δεν είναι απόλυτο. Χάσαμε την ουσία. Η αλήθεια ειναι οτι ο συνάδελφός σας φαίνεται να είναι εξαιρετικός εκπαιδευτικός και σίγουρα είστε και εσείς αλλα δεν δείξατε να το γνωρίζετε….Η εκπαίδευση δεν ειναι μονο Εγκυκλοπέδια.
Bildung hat sich in D leider zu Enzyklopädie und deren Anwendung zurückentwickelt. Normaler Weise hat jedes (Aus-) Bildungs- auch ein Erziehungsziel. Ich habe de Eindruck, heute wird man wieder auf Gehorsam und Obrigkeitshörigkeit getrimmt. Selber denken scheint unerwünscht zu sein.
η κατασκευη αυτη ως εποπτικο βοηθημα ειναι απλα καταπληκτικη. θελω να γκρινιαξω απο το ζορι μου που δεν το σκεφτηκα πρωτος να το κανω, τοσα χρονια στην εκπαιδευση αλλα λεω να μην το κανω.
Άστο καλύτερα. Τυχερός είσαι που δεν το έκανες γιατί θα αποδείκνυες ότι δεν είσαι στην εκπαίδευση, αλλά για εκπαίδευση.
οχι δεν ειμαι τυχερος, ειμαι εγκρατης, προσγειωμενος, και μη επι φραγμίτου του νότιου .ΕΙμαι στην εκπαιδευση και εχοντας τιθασευσει την επαρση μου γνωριζω οτι εκπαιδευοντας εκπαιδευομαι. αυτα ομως δεν αλλαζουν την πραγματικοτητα:η κατασκευη αυτη ως εποπτικο βοηθημα ειναι απλα καταπληκτικη.
Λοιπόν, αν όντως είσαι στην εκπάιδευση – που αφού με βεβαιώνεις το πιστεύω – πολλά εξηγούνται για την ποιότητα της εκπαίδευσης! Όταν ο δάσκαλος μόνον μιλάει χωρίς να ακούει καθόλου τι του λέει ο συνομιλητής του, αυτά είναι τα αποτελέσματα. Στου κουφού την πόρτα. Υγεία αγαπητέ με την τιθασευμένη έπαρση και λυπάμαι για την οξύτητα της λαϊκής ρήσης την οποία χρησιμοποίησα…
οντως οταν ο δάσκαλος μόνον μιλάει χωρίς να ακούει καθόλου τι του λέει ο συνομιλητής του, αυτά είναι τα αποτελέσματα
Για το λόγο αυτό είπα εξαρχής άπαξ “άστο καλύτερα”.
και πιαστο χειροτερα, αλλα η κατασκευη αυτη ως εποπτικο βοηθημα ειναι απλα καταπληκτικη.
Λίγο ακόμα και θα είσαι εσύ ο καταπληκτικός (για τραγούδι) με τις γαργάρες. Είδες που τελικά σου έκανε καλό η συνομιλία σου μαζί μου; Έτσι εκπαιδεύω εγώ. Με απτά αποτελέσματα. Ακόμα και τον μηχανικό τον κάνω αμήχανο. Δεν κρύβω ότι άρχισες να μου γίνεσαι ευχάριστος…
μην ξεχνας οτι εσυ αρχισες να συνομιλεις μαζι μου, για μια κατασκευη που ως εποπτικο βοηθημα ειναι απλα καταπληκτικη.
Τι μου θύμισες τώρα! Μα όλα τα θυμάσαι; Μάλλον το κάνεις επίτηδες για να με δυσκολέψεις; Για το καλό σου το έκανα γιατί κατάλαβα αμέσως ότι είσαι στην εκπαίδευση, λόγω του συμπεράσματος περί την υπόδειξη της περιπεπλεγμένης όσον και καταπληκτικής ταύτης υποδείξεως του εποπτικού βοηθήματος. Ξέρεις γίνεται και με μέλι η η καταπληκτική εφαρμογή, όσον και με ελαιόλαδο, αρκεί να είναι Καλαμών… Αν δεν είχες πάθει καταπληξία από την καταπληκτική αυτή εφαρμογή μπορεί να σε παρεξηγούσα.
επιτελους!! η δικαιωση και η αναγνωριση.
Εξαρχής θέλεις να πεις. Εξαρχής σε δικαίωσα και σε αναγνώρισα, μόνο που το έκανα λίγο περίπλοκο και δεν το κατάλαβες…
Επιτελους θελω πω, επιτελους. και μια και το αναφερατε και εγω εξαρχης σας καταλαβα και σας κατανοησα :)
Και εγώ «θέλω πω» δεν αμφιβάλλω.
αμα θελεις πει εσυ, δεν αμφιβαλλω οτι πεις οτι θελεις πεις
παρεπιπτοντως,η κατασκευη αυτη ως εποπτικο βοηθημα ειναι απλα καταπληκτικη.
“Παρεμπιπτόντως” θέλεις να πεις.
chat κάνετε εσείς οι δύο ;;
τώρα μπορεί να είναι κ ζευγάρι μετά απο δυο χρόνια…
Τα μαθηματικά δεν είναι ταχυδακτυλουργία. Με γυμνό οφθαλμό διαπιστώνεται ότι το τετράγωνο της υποτείνουσας δεν παράγεται από την υποτείνουσα του ορθογωνίου τριγώνου. Το ορθογώνιο τρίγωνο (κίτρινο) έχει μικρότερη πλευρά, αφού στα πλάγια υπάρχουν κενά να διέρχεται το νερό, από τις άλλες τρεις πλευρές του τετραγώνου στο οποίο η υποτείνουσα του τριγώνου συμμετέχει σαν μία από τις πλευρές του. Το τετράγωνο έχει 4 ίσες πλευρές και όχι 3 και μία μικρότερη. Η ακρίβεια υποτίθεται ότι είναι το καμάρι των μαθηματικών και εν προκειμένω είναι χοντροκομμένο το σφάλμα.
Θα διαφωνήσω μαζί σου. Στην κατασκευή δεν είναι απαραίτητο ότι υπάρχουν κενά που δημιουργούνται από άνισες πλευρές (ούτως ή άλλως δεν φαίνεται κάτι τέτοιο). Το κενό φαίνεται να υπάρχει από κάτω, δηλαδή στο βάθος. Έτσι κι αλλιώς, αν η κατασκευή δεν ήταν ακριβής, δε θα ήταν αυτό το αποτέλεσμα, σύμφωνα με το πυθαγόρειο θεώρημα!
Στην κατασκευή είναι απαραίτητο να υπάρχουν τα κενά γιατί χωρίς κενά δεν μπορεί να περάσει το νερό! Ωστόσο δεν είναι αυτό το θέμα. Το πυθαγόρειο όπως και κάθε κατσκευή στη γεωμετρία γίνεται αποκλειστικά με κανόνα και διαβήτη. Με αυτή τη μέθοδο (ρευστά) αποδεικνύεται “κατασκευαστικά” και ο τετραγωνισμός του κύκλου και λύνεται και το δήλιο πρόβλημα του διπλασιασμού του κύβου. Μη διαφωνείς λοιπόν. Είναι κακόγουστη αντίληψη (για να μη τη χαρακτηρίσω αντίληψη αδαούς) περί το πυθαγόρειο και την γεωμετρία γενικότερα.
Και ξανά: τα κενά φαίνεται να είναι από κάτω, δεν είναι κάποια πλευρά πιο μικρή. Τουλάχιστον έτσι φαίνεται, αν παρακολουθήσεις και τη ροή του νερού. Η μόνη κριτική που θα μπορούσα να κάνω σε αυτό ως “απόδειξη” (παρατήρηση που δεν έκανα η ίδια) είναι ότι το τρίγωνο θα έπρεπε να ήταν διαφανές, για να φαίνεται ότι δεν “κρύβεται” νερό από κάτω του.Η τελευταία σου πρόταση είναι κάπως αγενής. Οι χαρακτηρισμοί μπορούν να λείπουν.
Δεν ήθελα να σας προσβάλω και αν έτσι αντιληφθήκατε παρά το ότι δεν είναι αληθές, εκφράζω τη λύπη μου και ζητώ συγγνώμη. Επί της ουσίας: Δεν δείχνετε και τόση προσοχή (αυτό προσβάλει εμένα που συνομιλώ μαζί σας εντελώς καλοπροαίρετα) στις παρατηρήσεις μου πως το πυθαγόρειο (όπως και κάθε κατασκευή) ανήκει στα μαθηματικά μόνον αν αποδειχθεί με κανόνα και διαβήτη. Πέρα από αυτό το πυθαγόρειο θεώρημα είναι λάθος μέσω των κατασκευών ακόμα και με κανόνα και διαβήτη. Είστε δικαιολογημένη να μη το γνωρίζετε γιατί αποκρύπτετε και αυτό που λέω δεν είναι γενικό και αόριστο. Ωστόσο ευχαρίστως να σας βοηθήσω αν βέβαια το επιθυμείτε: ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑΑθήνα 2 Απριλίου 2007 Αρ. Πρωτοκόλλου: 12234/2-4-07 Ο κύριος Λάμπρος Θ. Μαγκλάρας απευθύνθηκε στην ΕλληνικήΜαθηματική Εταιρεία καταθέτοντας τον ισχυρισμό, ότι το πυθαγόρειο θεώρημα είναι εσφαλμένο.Επικαλέστηκε τα εξής:1. Ότι κατασκευαστικά δεν μπορεί να αποδειχθεί το θεώρημα, επειδή κατά τους μετασχηματισμούς είναι αδύνατο 2 ζεύγη κατακορυφήν γωνιών – π.χ. 2 ζεύγη ίσων μεταξύ τους ορθογωνίων ισοσκελών τριγώνων – να εφάπτονται ταυτόχρονα στο «κέντρο» του υπό σύνθεση τετραγώνου, ώστε να το αποτελέσουν.2. Ότι θεωρητικά το πυθαγόρειο θεώρημα:α. Ζητά και προβαίνει προς απόδειξή του, σε αθροίσειςσχημάτων (Το άθροισμα των τετραγώνων κ.τ.λ.) που δεν προβλέπονται από το αξιωματικό σύστημα του Ευκλείδη, ούτε από την νεότερη τυποποίησή του από τον Hilbert. β. Δεν έχει την αναγκαία για κάθε θεώρημα αξιωματικήστήριξη. Η Ελληνική Μαθηματική Εταιρεία, ανταποκρινόμενη με ευθύνη στις αιτιάσεις του κυρίου Λάμπρου Θ. Μαγκλάρα, θεωρώντας ταυτόχρονα χρέος τηςνα διαλευκάνει το ζήτημα, τον κάλεσε στην Επιτροπή ΕΥΚΛΕΙΔΗΣ Β΄ και παρουσία πλήθους συναδέλφων μαθηματικών καθηγητών, του παρέσχε τις εξής διευκρινήσεις σχετικά με το πυθαγόρειο θεώρημα. 1. Σε σχέση με την κατασκευαστική αδυναμία, που όντωςεμφανίζεται επί εποπτικής φύσεως, π.χ. υλικά υποδείγματα, όπως ορθά και ο ίδιοςεπισημαίνει, αυτή η αδυναμία ουδόλως επηρεάζει την ορθότητα του πυθαγορείου,καθώς η κατασκευή είναι εποπτική και τα μαθηματικά λειτουργούν αφαιρετικά τηςφύσης.2. Σε σχέση με τις αθροίσεις σχημάτων, του επισημάνθηκε, ότι όντως αυτές δεν προβλέπονται (όπως ορθά ισχυρίζεται) από την γεωμετρία, αλλάκατά ερμηνεία, οι αθροίσεις αυτές ανάγονται σε αθροίσεις εμβαδών, δηλονότι αριθμών και όχι σχημάτων. Έτσι, επί ορθογωνίου ισοσκελούς τριγώνου, με μέτρο κάθετης πλευράς 1, το τετράγωνο της υποτείνουσας εκφράζεται από τον ακέραιοθετικό αριθμό 2, δηλαδή από τετράγωνο με εμβαδόν 2.3. Σε σχέση με την αξιωματική στήριξη του πυθαγορείου, αυτή υποδείχθηκε στον κύριο Λάμπρο Θ. Μαγκλάρα, ότι ευρίσκεται στο αξίωμα του εμβαδού, αφού οι αθροίσεις είναι αθροίσεις εμβαδών και όχι σχημάτων.ΓΙΑ ΤΗΝ ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Ο εισάγων την ερμηνεία. ΠΡΟΕΔΡΟΣ ΕΚΤΕΛΕΣΤΙΚΗΣΓΡΑΜΜΑΤΕΙΑΣ ΕΥΚΛΕΙΔΗΣ Β΄Γιώργος ΤασσόπουλοςΠΡΟΕΔΡΟΣ ΕΜΕΝικόλαος Αλεξανδρής Να είσαστε καλά και αν έχετε απόδειξη του πυθαγόρειου στο πλαίσιο της θεωρίας συνόλων στην οποία ανήκει το αξίωμα του εμβαδού (αφού κάθε άλλη – όπως και η κατασκευή – δεν γίνεται δεκτή από την ΕΜΕ όπως διαπιστώνετε) ευχαρίστως να σας την ανατρέψω ομοίως, δηλαδή εύκολα. Σας ευχαριστώ για την ενδιαφέρουσα συνομιλία.