© 2026 ভিডিওম্যান | যোগাযোগ: info@videoman.gr | গোপনীয়তা নীতি | ব্যবহারের শর্তাবলী
প্লেয়ার লোড হচ্ছে...
জলের সাথে পিথাগোরিয়ান উপপাদ্যের প্রয়োগ
(42) | 30/12/2012 | একটি চতুর নির্মাণ যা জল দিয়ে পিথাগোরিয়ান উপপাদ্য প্রমাণ করে (একটি সমকোণী ত্রিভুজের কর্ণের বর্গ দুটি লম্ব বাহুর বর্গক্ষেত্রের সমষ্টির সমান).
একটি উত্তর ছেড়ে Lampros Th. মাগলার উত্তর বাতিল করুন
29 মন্তব্য
উন্নত সম্পর্কিত পোস্ট
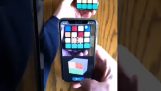
কিভাবে আমরা এটা করতে না? কি উপকরণ দিয়ে
এটা শুধু সরল জল. আপনি পিথাগোরিয়ান উপপাদ্য জানেন? এই যে উত্তর. (a2+b2=c2) মাঝখানে 3টি প্লেক্সিগ্লাস কিউব এবং একটি ত্রিভুজাকার রয়েছে, সে নিচের দুটিতে পানি ঢেলে দিল, কারণ টাই অনুযায়ী, কে c2 কিউব পূরণ করে, এই ব্যাখ্যা. পুথাগোরাস খুব স্মার্ট ছিলেন, তিনি এই উপপাদ্যটি আবিষ্কার করেছিলেন.
সত্যিই ভাল উপস্থাপনা আমি সত্যিই এটা পছন্দ. উপায় দ্বারা এটি জন্য আপনাকে ধন্যবাদ.
উজ্জ্বল, উপস্থাপনার জন্য সবার আগে অভিনন্দন. আপনার সহকর্মী কেবল মন্তব্য করেছেন যে এটি শিক্ষার্থীদের বোঝার এবং মুখস্থ করার জন্য একটি দুর্দান্ত উদাহরণ. আমি উজ্জ্বল বলব..কারণ এটি এত সহজ এবং পরিষ্কার. কেউ সঠিকতার প্রমাণের কথা বলেনি. এবং আপনি কল্পনা করুন যখন টেবিলের আকারগুলি গঠিত হয়, কিছুই পরম নয়. আমরা বিন্দু মিস. সত্য হল যে আপনার সহকর্মীকে একজন চমৎকার শিক্ষক বলে মনে হচ্ছে এবং অবশ্যই আপনিও কিন্তু আপনি এটা জানেন না যে আপনি এটা জানেন... শিক্ষা শুধুমাত্র বিশ্বকোষ নয়.
দুর্ভাগ্যবশত, জার্মানিতে শিক্ষা এনসাইক্লোপিডিয়া এবং তাদের প্রয়োগে ফিরে গেছে. সাধারণত সবারই থাকে (এর বাইরে-) শিক্ষামূলক- এছাড়াও একটি শিক্ষামূলক লক্ষ্য. আমি ছাপ আছে, আজ মানুষ আবার কর্তৃপক্ষের আনুগত্য ও আনুগত্য করার প্রশিক্ষণ পেয়েছে. নিজের জন্য চিন্তা করা অবাঞ্ছিত বলে মনে হচ্ছে.
একটি তত্ত্বাবধায়ক সাহায্য হিসাবে এই নির্মাণ সহজভাবে আশ্চর্যজনক. আমি প্রথমে এটি করার চিন্তা না করার জন্য আমার বোকামি সম্পর্কে অভিযোগ করতে চাই, এত বছর ট্রেনিং করছি কিন্তু বলছি না করতে.
এটা ভাল. আপনি ভাগ্যবান আপনি করেননি কারণ আপনি প্রমাণ করবেন আপনি প্রশিক্ষণে নেই, কিন্তু শিক্ষার জন্য.
না আমি ভাগ্যবান নই, আমি মধ্যপন্থী, অবতরণ, এবং দক্ষিণ বাধা উপর না. আমি প্রশিক্ষণে আছি এবং আমার অহংকারকে নিয়ন্ত্রণ করে আমি জানি যে প্রশিক্ষণের মাধ্যমে আমি প্রশিক্ষিত. যাইহোক, এগুলো বাস্তবতা পরিবর্তন করে না:একটি তত্ত্বাবধায়ক সাহায্য হিসাবে এই নির্মাণ সহজভাবে আশ্চর্যজনক.
ভাল, আপনি যদি সত্যিই শিক্ষায় থাকেন - যা আপনি আমাকে আশ্বস্ত করার পর থেকে আমি তাই বিশ্বাস করি - শিক্ষার মান সম্পর্কে অনেক কিছু ব্যাখ্যা করা হয়েছে! শিক্ষক যখন কথোপকথক যা বলছেন তা না শুনেই কেবল কথা বলেন, এই ফলাফল. দরজা বন্ধ কর. আমার অহংকারে চিয়ার্স, এবং আমি যে কথোপকথন ব্যবহার করেছি তার তীক্ষ্ণতার জন্য আমি দুঃখিত...
প্রকৃতপক্ষে, যখন শিক্ষক তার কথোপকথক যা বলছেন তা না শুনেই কেবল কথা বলেন, এই ফলাফল
তাই আমি শুরু থেকেই বলেছি 'এটা ভালো'.
এবং এমনকি খারাপ, কিন্তু একটি তত্ত্বাবধায়ক সাহায্য হিসাবে এই নির্মাণ শুধুমাত্র আশ্চর্যজনক.
একটু বেশি এবং আপনি আশ্চর্যজনক এক হবেন (গান গাওয়ার জন্য) gargles সঙ্গে. আপনি দেখেছেন যে আমার সাথে আপনার কথোপকথন সর্বোপরি আপনার ভাল হয়েছে; আমি এভাবেই ট্রেনিং করি. বাস্তব ফলাফল সঙ্গে. এমনকি ইঞ্জিনিয়ারও বিব্রত. আমি লুকাই না যে তুমি আমাকে খুশি করতে শুরু করেছ...
ভুলে যাবেন না যে আপনি আমার সাথে কথোপকথন শুরু করেছেন, একটি নির্মাণের জন্য যা একটি তদারকি সহায়তা হিসাবে কেবল আশ্চর্যজনক.
আপনি এখন আমাকে কি মনে করিয়ে দিলেন?! কিন্তু তোমার সব মনে আছে; আপনি সম্ভবত এটা আমার জন্য কঠিন করতে উদ্দেশ্যমূলকভাবে করছেন; আপনার জন্য আমি এটি করেছি কারণ আমি তখনই জানতাম যে আপনি প্রশিক্ষণে আছেন, জটিল এবং আশ্চর্যজনক এই ইঙ্গিত তত্ত্বাবধায়ক সহায়তার ইঙ্গিত সম্পর্কে উপসংহারের কারণে. আপনি জানেন যে এটি মধু বা আশ্চর্যজনক অ্যাপ্লিকেশন দিয়েও করা যেতে পারে, সেইসাথে জলপাই তেল দিয়ে, যতক্ষণ না এটি কালামন... আপনি যদি এই আশ্চর্যজনক অ্যাপ্লিকেশনটি দেখে হতবাক না হতেন তবে আমি আপনাকে ভুল বুঝতাম.
শেষ পর্যন্ত!! ন্যায্যতা এবং স্বীকৃতি.
আপনি প্রথম স্থানে বলতে চান. প্রথম থেকেই আমি আপনাকে ন্যায়সঙ্গত এবং চিনতে পেরেছি, ব্যতীত আমি এটিকে কিছুটা জটিল করেছি এবং আপনি এটি পাননি…
আমি সত্যিই বলতে চাই, শেষ পর্যন্ত. এবং যেহেতু আপনি এটি উল্লেখ করেছেন, আমি আপনাকে প্রথম থেকেই বুঝতে এবং বুঝতে পেরেছি :)
এবং আমি 'বলতে চাই' আমি সন্দেহ করি না.
যদি আপনি নিজে বলতে চান, আমি সন্দেহ করি না যে আপনি যা বলতে চান তা বলেছেন
ঘটনাক্রমে,একটি তত্ত্বাবধায়ক সাহায্য হিসাবে এই নির্মাণ সহজভাবে আশ্চর্যজনক.
'বাই দ্য ওয়ে' আপনি বলতে চান.
আপনারা দুজন চ্যাট করছেন ;;
এখন তারা দুই বছর পর দম্পতি হতে পারে...
গণিত জগাখিচুড়ি নয়. খালি চোখে দেখা যায় যে কর্ণের বর্গটি সমকোণী ত্রিভুজের কর্ণ দ্বারা উত্পাদিত হয় না।. সমকোণী ত্রিভুজ (হলুদ) একটি সংক্ষিপ্ত দিক আছে, যেহেতু পাশ দিয়ে পানি যাওয়ার জন্য ফাঁক রয়েছে, বর্গক্ষেত্রের অন্য তিনটি দিক থেকে যেখানে ত্রিভুজের কর্ণের একটি বাহু হিসেবে অংশ নেয়. বর্গক্ষেত্রে 3 এর পরিবর্তে 4টি সমান বাহু রয়েছে এবং একটি ছোট. নির্ভুলতা গণিতের গর্ব বলে মনে করা হয়, এবং এই ক্ষেত্রে ত্রুটি স্থূল.
আমি আপনার সাথে একমত হবে না. নির্মাণের ক্ষেত্রে এটি প্রয়োজনীয় নয় যে অসম পক্ষগুলির দ্বারা তৈরি ফাঁক রয়েছে (এটা যাইহোক যে ভাবে মনে হয় না). ফাঁকটি নীচে বিদ্যমান বলে মনে হচ্ছে, যে, পটভূমিতে. যাই হোক, যদি নির্মাণ সঠিক না হয়, এই ফলাফল হবে না, পিথাগোরিয়ান উপপাদ্য অনুসারে!
নির্মাণে ফাঁক থাকা দরকার কারণ ফাঁক ছাড়া জল যেতে পারে না! যাইহোক, যে বিন্দু না. পীথাগোরিয়ান, জ্যামিতির যে কোনো নির্মাণের মতোই, একচেটিয়াভাবে একটি নিয়ম এবং একটি কম্পাস দিয়ে করা হয়।. এই পদ্ধতি দিয়ে (তরল) বৃত্তের বর্গক্ষেত্রও 'গঠনমূলকভাবে' প্রমাণিত এবং ঘনক্ষেত্রকে দ্বিগুণ করার উন্মত্ত সমস্যাটিও সমাধান করা হয়েছে. তাই তর্ক করবেন না. এটা একটা খারাপ ধারণা (এটাকে অজ্ঞতাপূর্ণ ধারণা বলা যাবে না) সাধারণভাবে পিথাগোরাস এবং জ্যামিতি সম্পর্কে.
এবং আবার: ফাঁকগুলি নীচে প্রদর্শিত হবে, এটা কোন দিক ছোট নয়. অন্তত তাই মনে হয়, আপনি যদি পানির প্রবাহও দেখেন. 'প্রমাণ' হিসাবে আমি এটির একমাত্র সমালোচনা করতে পারি (একটি পর্যবেক্ষণ আমি নিজেকে তৈরি করিনি) ত্রিভুজটি স্বচ্ছ হওয়া উচিত ছিল, এটি দেখানোর জন্য যে কোনও জল এর নীচে 'লুকিয়ে' নেই। আপনার শেষ বাক্যটি কিছুটা অভদ্র. গুণাবলী অনুপস্থিত হতে পারে.
আমি আপনাকে অসন্তুষ্ট করতে চাইনি এবং আপনি যদি এইভাবে বুঝতে পারেন, যদিও এটি সত্য নয়, আমি আমার দুঃখ প্রকাশ করছি এবং ক্ষমাপ্রার্থী. বিন্দু পর্যন্ত: আপনি অতটা মনোযোগ দেন না (এটি আমাকে বিরক্ত করে যে আপনার সাথে সম্পূর্ণভাবে সরল বিশ্বাসে কথা বলে) আমার পর্যবেক্ষণে যে পিথাগোরিয়ান (যে কোনো নির্মাণের মতো) এটি গণিতের অন্তর্গত শুধুমাত্র যদি এটি নিয়ম এবং ডিগ্রাফ দ্বারা প্রমাণিত হয়. এর বাইরে পিথাগোরিয়ান উপপাদ্যটি একটি নিয়ম এবং একটি কম্পাস দিয়েও নির্মাণ দ্বারা মিথ্যা. আপনি না জানার জন্য যুক্তিযুক্ত কারণ আপনি লুকিয়ে আছেন এবং আমি যা বলছি তা সাধারণ এবং অস্পষ্ট নয়. যাইহোক, যদি আপনি চান আমি আপনাকে সাহায্য করতে খুশি: গ্রীক গাণিতিক সমাজ এথেন্স 2 এপ্রিল, 2007 না. প্রোটোকল: 12234/2-4-07 মিঃ ল্যামব্রোস থ. ম্যাগলারাস হেলেনিক ম্যাথমেটিকাল সোসাইটি দাবি করে বক্তব্য রাখেন, যে পিথাগোরিয়ান উপপাদ্যটি ভুল। তিনি নিম্নলিখিত আহ্বান জানান:1. যে উপপাদ্য নির্মাণ দ্বারা প্রমাণ করা যাবে না, কারণ রূপান্তরের সময় 2 জোড়া উল্লম্ব কোণগুলি অসম্ভব - যেমন. 2 জোড়া সমান সমকোণী সমদ্বিবাহু ত্রিভুজ - রচিত বর্গক্ষেত্রের 'কেন্দ্রে' একই সময়ে স্পর্শ করে, যাতে এটি গঠন করা যায়।2. যে তাত্ত্বিকভাবে পিথাগোরিয়ান উপপাদ্য:ক. তিনি জিজ্ঞাসা করেন এবং এটি প্রমাণ করতে এগিয়ে যান, আকারের সমষ্টিতে (বর্গক্ষেত্রের সমষ্টি ইত্যাদি।) যা ইউক্লিডের স্বতঃসিদ্ধ সিস্টেম দ্বারা ভবিষ্যদ্বাণী করা হয় না, বা হিলবার্ট এর পরে এটি আনুষ্ঠানিককরণের পর থেকেও নয়. খ. এটি প্রতিটি উপপাদ্যের জন্য প্রয়োজনীয় স্বতঃসিদ্ধ সমর্থন নেই. হেলেনিক ম্যাথমেটিকাল সোসাইটি, জনাব Lambros Th এর আপত্তির দায়িত্বের সাথে সাড়া. মাগলার, একই সাথে বিষয়টিকে স্পষ্ট করা তার দায়িত্ব বিবেচনা করে, তাকে ইউক্লাইডস II কমিটিতে এবং বিপুল সংখ্যক সহকর্মী গণিতের অধ্যাপকদের উপস্থিতিতে আমন্ত্রণ জানান।, পিথাগোরিয়ান উপপাদ্য সম্পর্কে তাকে নিম্নলিখিত ব্যাখ্যা প্রদান করেছেন. 1. উত্পাদনের অসম্ভবতার সাথে সম্পর্কিত, যা আসলে একটি সুপারভাইজরি ভিত্তিতে ঘটে, B.C. উপাদান নমুনা, যেমন তিনি সঠিকভাবে উল্লেখ করেছেন, এই দুর্বলতা কোনোভাবেই পিথাগোরিয়ানের সঠিকতাকে প্রভাবিত করে না,যেহেতু নির্মাণ তত্ত্বাবধায়ক এবং গণিত প্রকৃতিতে বিমূর্তভাবে কাজ করে. আকারের যোগফলের সাথে সম্পর্কিত, তাকে নির্দেশ করে, যে সত্যিই এই পূর্বাভাস হয় না (যেমন তিনি সঠিকভাবে দাবি করেছেন) জ্যামিতি থেকে, কিন্তু ব্যাখ্যা দ্বারা, এই সমষ্টিগুলিকে এলাকার সমষ্টিতে হ্রাস করা হয়, সংখ্যা এবং আকার না যদিও. তাই, একটি ডান সমদ্বিবাহু ত্রিভুজের উপর, উল্লম্ব পার্শ্ব পরিমাপ সঙ্গে 1, কর্ণের বর্গকে ধনাত্মক পূর্ণসংখ্যা 2 দ্বারা প্রকাশ করা হয়, অর্থাৎ, 2.3 এর ক্ষেত্রফল সহ একটি বর্গক্ষেত্র থেকে. পিথাগোরিয়ান স্বতঃসিদ্ধ সমর্থনের সাথে সম্পর্কিত, তাকে ইঙ্গিত করা হয়েছিল মিঃ ল্যামব্রোস থ. মাগলার, যেটি এলাকার স্বতঃসিদ্ধ, যেহেতু সমষ্টিগুলি ক্ষেত্রফলের সমষ্টি এবং আকারের নয়। গ্রীক গাণিতিক সমাজের জন্য ব্যাখ্যার প্রবর্তক. এক্সিকিউটিভ সেক্রেটারিয়েটের চেয়ারম্যান ইউক্লিডস II জিওরগোস টাসোপোলোস চেয়ারম্যান ইমেনিকোলাওস আলেকজান্দ্রিস আপনার কাছে যদি সেট তত্ত্বের প্রেক্ষাপটে পিথাগোরিয়ানের প্রমাণ থাকে যা এলাকার স্বতঃসিদ্ধ। (যেহেতু আপনি দেখতে পাচ্ছেন যে অন্য কোনো - যেমন নির্মাণ - EME দ্বারা গৃহীত হয় না) আমি আপনার জন্য এটি বিপরীত হিসাবে খুশি হবে, যে, সহজে. আকর্ষণীয় কথোপকথনের জন্য আপনাকে ধন্যবাদ.